Eigenfunctions and eigenvalues of modified double-center Woods-Saxon potential
Keywords:
Modified Woods-Saxon potential, Schrodinger equation, Eigenfunctions, Nikiforov-Uvarov methodAbstract
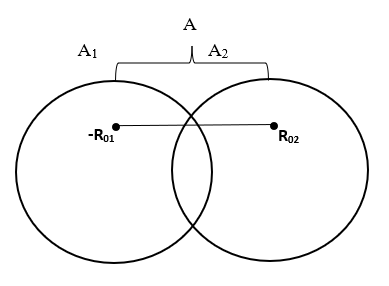
This study explores the quantum mechanical dynamics of nuclear fission of uranium-235 using a modified double-center Woods-Saxon potential. The Schrödinger equation is solved via the Nikiforov-Uvarov method to derive eigenfunctions and eigenvalues characterizing the fission process. The research models binary fission to reveal subatomic phenomena such as energy transitions and particle probabilities during nucleus splitting process. By solving the radial component of the three-dimensional Schrödinger equation, the study computes eigenfunctions, eigenvalues, and probability densities, providing insights into the nuclear system's quantum states. The key aspects examined include energy level transitions, the influence of eccentricity, and double-fold degeneracies. Results illustrate the dynamic evolution of fragment separation, transitioning from overlap at equilibrium to distinct potential wells as fragments become independent. The eigenfunctions exhibit even parity π⁺ for eigenvalues n_z = 0, 2, 4, 6 and odd parity π⁻ for n_z = 1, 3, 5, 7, with the number of nodes reflecting their states. Energy eigenvalues are determined by applying continuity conditions at the boundary (z = 0) and solving transcendental equations across various eccentricity values. The eigenvalue spectrum reveals double-fold degeneracy, indicating a transition from two independent schemes to a single configuration at infinite separation, describing the complete asymmetric fission of ²³⁵U into two fragments. These findings of the research underscore the model's capability to depict fission dynamics, offering significant insights into nuclear interactions, energy transitions, and the mechanics of heavy nuclei splitting. The study highlights the potential of modified double-center Woods-Saxon potentials in advancing our understanding of nuclear binary fission processes.
Published
How to Cite
Issue
Section
Copyright (c) 2025 Emmanuel Vezua Tikyaa, Emmanuel Damian Adukwu, Idugba Mathias Echi, Solomon Denen Igba

This work is licensed under a Creative Commons Attribution 4.0 International License.
How to Cite
Most read articles by the same author(s)
- Tertsea Igbawua, Aondongu Alexander Tyovenda, Terver Sombo, Idugba Mathias Echi, Fanan Ujoh, Investigating factors influencing PM2.5 threshold exceedance in Nigeria using multivariate logistic regression analysis , African Scientific Reports: Volume 3, Issue 3, December 2024
- Emmanuel Ike, Adetola Sunday Oniku, Sabastine Chinedu Ezike, Maxwell Obia Kanu, Rodney Ewusi-Wilson, Geothermal resource potentials estimation from the interpretation of aeromagnetic data over parts of Southwestern Nigeria , African Scientific Reports: Volume 3, Issue 1, April 2024
- Emmanuel Joseph, Gonto Kamal, Oluwasesan M. Bello, Natural radionuclide distribution and analysis of associated radiological concerns in rock samples from a rocky town (Dutsin-Ma) in the North-Western region of Nigeria , African Scientific Reports: Volume 2, Issue 3, December 2023
- Solomon Denen Igba, Idugba Mathias Echi, Emmanuel Vezua Tikyaa, Simulation of thermochemical effects on unsteady magneto hydrodynamics fluids flow in two dimensional nonlinear permeable media , African Scientific Reports: Volume 3, Issue 3, December 2024
- Terver Sombo, Titus Nyitar, Emmanuel Vezua Tikyaa, Tertsea Igbawua, Investigation of diurnal road traffic noise in Makurdi metropolis, Benue State, Nigeria , African Scientific Reports: Volume 4, Issue 2, August 2025
- A. I. Bassey, M. A. Agana, E. A. Edim, O. Njama-Abang, Intrusion detection in a controlled computer network environment using hybridized random forest and long short-term memory algorithms , African Scientific Reports: Volume 4, Issue 3, December 2025 (In Progress)




