Robust-M new two-parameter estimator for linear regression models: Simulations and applications

Authors

  • Taiwo J. Adejumo Department of Statistics, Ladoke Akintola University of Technology, Ogbomoso, Oyo State, Nigeria
  • Kayode Ayinde Department of Statistics, Federal University of Technology, Akure, Nigeria; Department of Mathematics and Statistics, Northwest Missouri State University, Maryville, Missouri, USA
  • Abayomi A. Akomolafe Department of Statistics, Federal University of Technology, Akure, Nigeria
  • Olusola S. Makinde Department of Statistics, Federal University of Technology, Akure, Nigeria
  • Adegoke S. Ajiboye Department of Statistics, Federal University of Technology, Akure, Nigeria

Keywords:

Ordinary least squares, Multicollinearity, Outliers, Estimators, Simulation study

Abstract

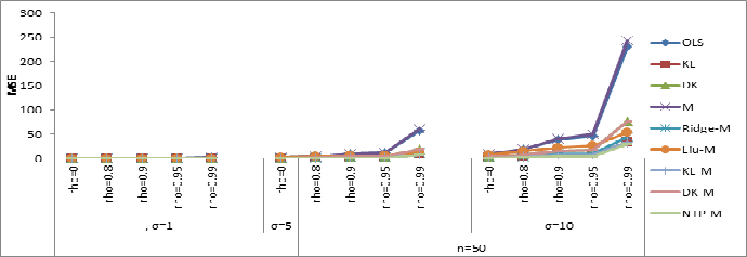
In the presence of multicollinearity and outliers, the ordinary least squares estimator remains inconsistent and unreliable. Several estimators have been proposed that can co-handle the problems of multicollinearity and outliers simultaneously. However, there is still a need to explore some other robust methods when the two anomalies appear in the linear regression model and recommend it to end users of statistics. Therefore, this study proposed Robust-M New Two Parameter (RNTP) and examined its performance over some already existing ones in the presence of multicollinearity and outliers in the x-direction. The theoretical expression under some conditions was established to showcase the new estimator's superiority. A simulation study was carried out alongside some factors to show that the RNTP is better than all other estimators considered in the study. The simulation study results revealed that RNTP outperformed other estimators in the study using the minimum MSE as the criterion. Likewise, real-life data was applied to affirm this claim.

Dimensions

P. J. Hurber, “Robust estimation of a location parameter”, The Annals of Mathematical Statistics 35 (1964) 73. https://doi.org/10.1214/aoms/1177703732

V. J. Yohai, “High breakdown-point and high-efficiency robust estimates for regression”, The Annals of Statistics 15 (1987) 642. https://doi.org/10.1214/aos/1176350366

P. J. Rousseeuw & V. K. Driessen, “Computing LTS regression for large data sets”, Technical Report University of Antwerp submitted, (1998). https://doi.org/10.1007/s10618-005-0024-4

P. J. Rousseeuw & V.J. Yohai, “Robust regression by means of S-estimator”, In W. H. J. Frank and D. Martin; Robust and nonlinear Time series Analysis, Springer-verlag, New York, 1984, pp. 256 – 272. https://doi.org/10.1007/978-1-4615-7821-5 15

P. J. Rousseeuw, “Least median of squares regression”, Journal of the American Statistical Association 79 (1984) 871. https://doi.org/10.1080/01621459.1984.10477105

D. Birkes & Y. D. Dodge, Alternative methods of regression, Wiley, New York, 1993. https://www.wiley.com/en-us/Alternative+Methods+of+Regression-p-9781118150245

A. T. Owolabi, K. Ayinde, & O. O. Alabi, A new ridge-type estimator for the linear regression model with correlated regressors, Wiley, 2022. https://doi:10.1002/cpe.6933

A. E. Hoerl, & R. W. Kennard, “Ridge Regression. Biased Estimation for nonorthogonal problems”, Technometrics 1 (1970) 55. https://homepages.math.uic.edu

W. F. Massy, “Principal components regression in exploratory statistical research”, Journal of America Statistics Association 60 (1965) 234. https://doi.org/10.2307/2283149

C. Stein, “Inadmissibility of the usual estimator for the mean of a multivariate normal distribution”, Proceedings of the third Berkeley symposium on Mathematical statistics and probability 1 (1956) 197. https://projecteuclid.org/ebooks/berkeley-symposium-on-mathematical-statistics-and-probability/Proceedings-of-the-Third-Berkeley-Symposium-on-Mathematical-Statistics-and/chapter/Inadmissibility-of-the-Usual-Estimator-for-the-Mean-of-a/bsmsp/1200501656

K. Liu, “A new class of biased estimate in linear regression”, Journal of Communications in statistics: Theory and Methods 22 (1993) pp. 393. https://doi.org/10.1080/03610929308831027

S. Dawoud, M. R. Abonazel & F. A. Awwad, “Generalized Kibria-Lukman estimator: method, simulation and application”, Frontiers in Applied Mathematics and Statistics 8 (2022) 880086. https://doi.org/10.3389/fams.2022.880086

A. F. Lukman, O. Arowolo, & K. Ayinde, “Some robust ridge regression for handling multicollinearity and outliers”, International Journal of Sciences: Basic and Applied Research (IJSBAR) 16 (2014) 192. https://core.ac.uk/download/pdf/249333933.pdf

F. A. Awwad, I. Dawoud, & M. R. Abonazel, “Development of robust Ozkale Kaciranlar and Yang-Chang estimators for regression models in the presence of multicollinearity and outliers”, Concurr Comput Prac Exp. 34 (2022) e6779. https://doi.org/10.1002/cpe.6779

I. Dawoud & M. R. Abonazel, “Robust Dawoud-Kibria estimator for handling multicollinearity and outliers in the linear regression model”, Journal of Statistical Computation and Simulation 91 (2021) 3678. https://doi.org/10.1080/00949655.2021.1945063

E. A. Hassan, “Modified ridge M-estimator for linear regression model with multicollinearity and outliers”, Communication in Statistics and Computation 47 (2017) 1240. https://doi.org/10.1080/03610918.2017.1310231

M. J. Silvapulle, “Robust ridge regression based on an M-estimator”, Australian Journal of Statistics 33 (1991) 319. https://doi.org/10.1111/j.1467-842X.1991.tb00438.x

O. Arslan, & N. Billor, “ Robust Liu estimator for regression based on an M-estimator”, Journal Applied Statistics 27 (2000) 39. https://doi.org/10.1080/02664760021817.

B. M. Kibria & A. F. Lukman, “A new ridge-type estimator for the linear regression model”, Simulations and Applications, Hindawi scientifica 2020 (2020) 9758378. https://doi.org/10.1155/2020/9758378

A. Majid, S. Ahmad, M. Aslam, & M. A. Kashif, “Robust Kibria-Lukman estimator for linear regression model to combat multicollinearity and outliers”, Concurrency and Computation: Practice and Experience 35 (2022) e7533. https://doi.org/10.1002/cpe.7533

M. R. Ozkale,& S. Kaciranlar, “The restricted and unrestricted two-parameter estimators”, Communication Statistics. Theory. Meth. 36 (2007) 2707. https://doi.org/101080/036109207013868

S. S. F. Kaciranlar, G. P. H. S. Akdeniz, & H. J. Werner, “A new biased estimator in linear regression and detailed analysis of the widely-analysed dataset on Portland Cement”, Indian Statistical Institute 61 (1999) 443. https://www.jstor.org/stable/25053104

F. R. Hampel,, E. M. Ronchetti, P. J. Rousseeuw, & W. A. Stahel. Robust statistics, the approach based on inference function, Wiley, New York, 1986. https://www.wiley.com/en-us/Robust+Statistics%3A+The+Approach+Based+on+Influence+Functions-p-9781118150689

P. J. Hubber, Robust statistics, Wiley, New York, 1981. https://doi.org/10.1002/0471725250.

H. Yang & X. Chang, “A new two-parameter estimator in linear regression model”, Communication in Statistics. Theory and Methods 39 (2010) 923. https://doi.org/10.1080/03610920902807911.

A. F. Lukman,, K. Ayinde, B. B. Aladeitan, & B. Rasak, “An unbiased estimator with prior information”, Arab Journal of Basic and Applied Sciences. 27 (2020) 45. https://doi.org/10.1080/25765299.2019.1706799

Y. E. Hussein & A. A. Abdalla, “Generalized two stage ridge regression estimator GTR for multicollinearity and autocorrelated errors”, Canadian Journal of Science and Engineering Mathematics 3 (2012) 79. https://www.researchgate.net/publication/283205493 Generalized Two Stages Ridge regression Estimator GTR for Multicollinearity and Autocorrelated Errors

H. Midi & M. Zahari, “A simulation study on ridge regression estimators in the presence of outliers and multicollinearity”, Journal of Teknologi 47 (2007) 59. https://doi.org/10.11113/JT.V47.261

Published

2023-11-11

How to Cite

Robust-M new two-parameter estimator for linear regression models: Simulations and applications. (2023). African Scientific Reports, 2(3), 138. https://doi.org/10.46481/asr.2023.2.3.138

Issue

Volume 2, Issue 3, December 2023

Section

Original Research
Copyright & Licensing

Copyright (c) 2023 Taiwo J. Adejumo, Kayode Ayinde, Abayomi A. Akomolafe, Olusola S. Makinde, Adegoke S. Ajiboye

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Robust-M new two-parameter estimator for linear regression models: Simulations and applications. (2023). African Scientific Reports, 2(3), 138. https://doi.org/10.46481/asr.2023.2.3.138