A Modified Two Parameter Estimator with Different Forms of Biasing Parameters in the Linear Regression Model

Authors

  • Abiola T. Owolabi Department of Statistics, Ladoke Akintola University of Technology, Ogbomoso, Oyo State, Nigeria
  • Kayode Ayinde Department of Statistics, Federal University of Technology, Akure, Nigeria
  • Olusegun O. Alabi Department of Statistics, Federal University of Technology, Akure, Nigeria

Keywords:

Ridge estimator, Liu estimator, Multicollinearity, Mean square error, Kibria-Lukman estimator, Prior iInformation

Abstract

Despite its common usage in estimating the linear regression model parameters, the ordinary least squares estimator often suffers a breakdown when two or more predictor variables are strongly correlated. This study proposes an alternative estimator to the OLS and other existing ridge-type estimators to tackle the problem of correlated regressors (multicollinearity). The properties of the proposed estimator were derived, and six forms of biasing parameter k (generalized, median, mid-range, arithmetic, harmonic and geometric means) were used in the proposed estimator to compare its performance with five other existing estimators through a simulation study. The proposed estimator dominated existing estimators when the mid-range, arithmetic mean, and median versions of k were used. However, the proposed estimator did not perform well when the generalized, harmonic, and geometric
mean versions were used.

Dimensions

T. S. Ac¸ar & M. R. O¨ zkale, “Regression diagnostics methods for Liu estimator under the general linear regression model,” Communications in Statistics - Simulation and Computation 49 (2019) 3.

A. E. Hoerl & R. W. Kennard, “Ridge regression: biased estimation for nonorthogonal problems”, Technometrics 12 (1970) 55.

C. Stein, Inadmissibility of the usual estimator for mean of multivariate normal distribution,“ in Proceedings of the 0ird Berkley Symposium on Mathematical and Statistics Probability., J. Neyman, Ed., Berlin: Springer (1956) 1.

W. F. Massy, “Principal components regression in exploratory statistical research”, Journal of the American Statistical Association 60 (1965) 234.

B. F. Swindel, “Good ridge estimators, based on prior information”, Communications in Statistics - Theory and Methods 5 (1976) 1065

L. S. Mayer & T.A.Willke, “On biased estimation in linear models”, Technometrics 15 (1973) 497.

K. Liu, “A new class of biased estimate in linear regression”, Communications in Statistics 22 (1993) 393.

B. M. G. Kibria & A. F.Lukman, “A New Ridge-Type Estimator for the Linear Regression Model: Simulations and Applications”, Hindawi Scientifica (2020) 16.

M. R. Ozkale & S. Kac¸iranlar, “The restricted and unrestricted two-parameter estimators”, Communications in Statistics-Theory and Methods 36 (2007) 2707.

H. Yang & X. Chang, “A new two-parameter estimator in linear regression”, Communications in Statistics-Theory and Methods 39 (2010) 923.

A. V. Dorugade, “Modified two parameter estimator in linear regression”, Statistics in Transition New Series 15 (2014) 23.

M. Roozbeh, “Optimal QR-based estimation in partially linear regression models with correlated errors using GCV criterion”, Computational Statistics & Data Analysis 117 (2018) 45.

K. Ayinde, A. F. Lukman, O. O. Samuel & S.A. Ajiboye, “Some new adjusted ridge estimators of linear regression model”, Int. J. Civ. Eng. Technol. 9 (2018) 2838.

A. F. Lukman, K. Ayinde, S. Binuomote&O. A. Clement, “Modified ridge-type estimator to combat multicollinearity: application to chemical data”, Journal of Chemometrics 33 (2019) e3125.

I. Dawoud & B. M. G. Kibria, “A New Biased Estimator to Combat the Multicollinearity of the Gaussian Linear Regression Model”, Stats 3 (2020a) 526.

O. J. Oladapo, A. T. Owolabi, J. I. Idowu & K. Ayinde, “A New Modified Liu Ridge-Type Estimator for the Linear Regression Model: Simulation and Application”, Int J Clin Biostat Biom. 8 (2022).

A. T. Owolabi, K. Ayinde & O. O. Alabi, “A New Ridge-Type Estimator for the Linear Regression Model with correlated regressors”, Concurrency and Computation: Practice and Experience (2022) CPE6933.

A. T. Owolabi, K. Ayinde, J. I. Idowu, O. J. Oladapo & A. F. Lukman, “A New Two-Parameter Estimator in the Linear Regression Model with Correlated Regressors”, Journal of Statistics Applications & Probability 11 (2022) 499.

T. S. Fayose & K. Ayinde, ”Different Forms Biasing Parameter for Generalized Ridge Regression Estimator”, International Journal of Computer Applications 181 (2019) 975.

R. Farebrother, “Further results on the mean square error of ridge regression”, J. R. Stat. Soc. B 38 (1976).

G. Trenkler & H. Toutenburg, “Mean squared error matrix comparisons between biased estimators-an overview of recent results”, Stat Pap. 31 (1990) 165.

B. M. G. Kibria, “Performance of some new ridge regression estimators”, Communications in Statistics-Simulation and Computation 32 (2003) 419.

A. F. Lukman, K. Ayinde, S. K. Sek & E. Adewuyi, “A modified new two-parameter estimator in a linear regression model”, Modelling and Simulation in Engineering (2019) 6342702.

I. Dawoud & B. M. G. Kibria, “A New Two Parameter Biased Estimator for the Unrestricted Linear Regression Model: Theory, Simulation, and Application”, Int J Clin Biostat Biom. 6 (2020b).

F. Akdeniz & S. Kaciranlar, “On the almost unbiased generalized Liu estimator and unbiased estimation of the bias and MSE”, Communications in Statistics-Theory and Methods 24 (1995) 1789.

S. Kaciranlar, “Liu estimator in the general linear regression model,” Journal of Applied Statistical Science 13 (2003) 229.

M. I. Alheety & B. M. G. Kibria, “On the Liu and almost unbiased Liu estimators in the presence of multicollinearity with heteroscedastic or correlated errors”, Surveys in Mathematics and Its Applications 4 (2009) 155.

G. Shukur, K. Månsson & P. Sjolander, “Developing Interaction Shrinkage Parameters for the Liu Estimator—with an Application to the Electricity Retail Market”, Computational Economics 46 (2015) 539.

M. Qasim, M. Amin & M.A. Ullah, “On the performance of some new Liu parameters for the gamma regression model”, Journal of Statistical Computation and Simulation 88 (2018) 3065.

K. Månsson, B. M. G. Kibria & G. Shukur, “A new Liu type of estimator for the restricted SUR estimator”, Journal of Modern Applied Statistical Methods 18 (2019) eP2758,.

A.F. Lukman & K. Ayinde, “Review and classifications of the ridge parameter estimation techniques”, Hacettepe Math Stat. 46 (2017) 953.

G. C. McDonald & D. I. Galarneau, “A Monte Carlo evaluation of some ridge-type estimators”, Journal of the American Statistical Association 70 (1975) 407.

D. W. Wichern & G. A. Churchill, “A comparison of ridge estimators”, Technometrics 20 (1978) 301.

D. G. Gibbons, “A simulation study of some ridge estimators”, Journal of the American Statistical Association 76 (1981) 131.

A. F. Lukman, K. Ayinde, B. Aladeitan & R. Bamidele, “An unbiased estimator with prior information”, Arab Journal of Basic and Applied Sciences 27 (2020) 45.

L. L. Firinguetti, “A simulation study of ridge regression estimators with autocorrelated errors”, Communications in Statistics Simulation and Computation 18 (1989) 673.

J. P. Newhouse & S. D. Oman, “An evaluation of ridge estimators. A report prepared for United States air force project RAND”, (1971).

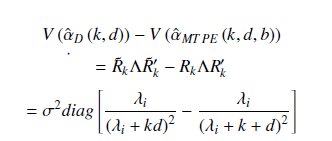
Published

2022-12-29

How to Cite

A Modified Two Parameter Estimator with Different Forms of Biasing Parameters in the Linear Regression Model. (2022). African Scientific Reports, 1(3), 212–228. https://doi.org/10.46481/asr.2022.1.3.62

Issue

Volume 1, Issue 3, December 2022

Section

Original Research
Copyright & Licensing

Copyright (c) 2022 Abiola T. Owolabi, Kayode Ayinde, Olusegun O. Alabi

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

A Modified Two Parameter Estimator with Different Forms of Biasing Parameters in the Linear Regression Model. (2022). African Scientific Reports, 1(3), 212–228. https://doi.org/10.46481/asr.2022.1.3.62