Convective Flow of Blood through a Constricted Cylinder and the Effect of Cholesterol Growth Rate on the Motion in the Presence of a Magnetic Field
Keywords:
Blood, Convection, Cholesterol, Growth, Motion, Magnetic Field, Cylinder, LDLAbstract
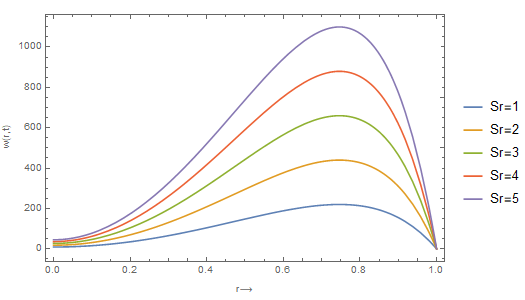
An inflammatory disease resulting in the pathological constriction of the intima and media of the arterial system, such as the aorta, causes symptoms like stroke, heart attack, or angina; This research investigates the convective flow of blood through a constricted cylinder and the effect of cholesterol growth rate on the motion in the presence of a magnetic field by transforming the problem into a system of time-dependent partial differential equations. The governing partial differential equations (PDEs) were transformed into dimensionless ordinary differential equations (ODEs) and solved using the Laplace method. After obtaining the analytical solution, Wolfram Mathematica was used to perform the numerical computation where the various physical parameters such as Soret number, radiation number, solutal Grashof number, Schmidt number, and Prandtl number were varied to their impact studied. The study discovered that increasing the Soret number causes an increase in blood velocity, whereas decreasing the Solutal Grashof number decreases blood velocity. Furthermore, an increase in radiation parameter increases the blood velocity, but a Soret number increase results in a decrease in the concentration of cholesterol in the fluid, a Schmidt number, and oscillatory frequency increase, causing the temperature to decrease. This research is useful for clinicians and mathematical modellers who are trying to understand the flow of cholesterol saturated fluid in the human vascular system and how best to proffer analytical and numerical solutions in synergy with laboratory investigation.
Published
How to Cite
Issue
Section
Copyright (c) 2022 K. W. Bunonyo, E. Amos

This work is licensed under a Creative Commons Attribution 4.0 International License.



