Approximate solution of time-fractional non-linear parabolic equations arising in Mathematical Physics
Keywords:
Iterative method, Gamma function, Parabolic equationAbstract
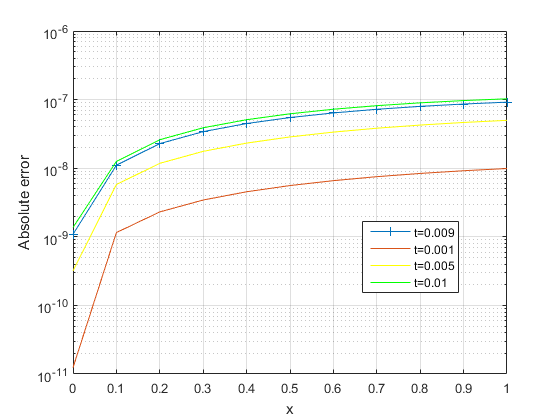
In this paper, we studied and analysed a new iterative method for solving time-fractional non-linear equations by obtaining approximate solutions to the Allen-Cahn, Newell-Whitehead, and Fisher equations by putting the parameter \alpha = 1 and varying the values of \gamma, \phi, and \tau. These three equations were derived from the general non-linear dynamical wave equations when the constants therein assumed certain specific values. Obviously, from the tabulated results, we observed that the approximate solution for each example compares favourably with the existing results in the literature; therefore, the proposed scheme is effective and accurate in solving Allen-Cahn, Newell-Whitehead, and Fisher equations. All the computational work was done using Mathematica, and all the graphs were plotted using MATLAB.
Published
How to Cite
Issue
Section
Copyright (c) 2024 K. Issa, R. A. Bello, M. H. Sulaiman

This work is licensed under a Creative Commons Attribution 4.0 International License.



