Analysis of Varroosis Model in Honeybee Colony with Interventions

Authors

  • Ahmed Umar Department of Mathematics, Modibbo Adama University, P.M.B 2076, Yola, Nigeria
  • Samuel Musa Department of Mathematics, Modibbo Adama University, P.M.B 2076, Yola, Nigeria
  • Andrew Apeh Agada Department of Mathematics, Skyline University Nigeria, Kano, Nigeria

Keywords:

Bifurcation, Global stability, Sensitivity analysis and Honeybee colony

Abstract

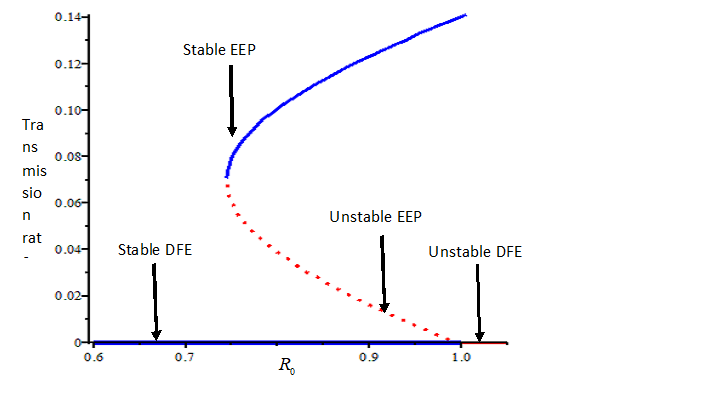
A deterministic mathematical model is proposed and analyzed to study the transmission dynamics of Varroosis in honeybee colony with interventions. The study combined both treatment and biocontrol strategy on curbing the menace of Varroosis on honeybee colony. As such, the study established the existence of the most important four steady states that include: disease-free and infestation-free, infestation with virus-free Varroa-mites, infestation with virus-carrying Varroa-mites and endemic steady state. Moreover, the study established the existence of backward bifurcation and sensitivity analysis of the model was performed. Correspondingly, the analysis of the model reveals that, ineffective treatment can induce backward bifurcation. Furthermore, the study results indicated that, when treatment is 100% effective, the disease-free and infestation-free steady state is globally asymptotically stable for R0 < 1, whereas for R0 > 1the global stability of the endemic steady state is proved only on a special case.

Dimensions

M. Klein, B. Vaissiere, J. Cane, I. Ste an-Dewenter, S. Cunningham, C. Kremen & T. Tscharntke, “Importance of pollinators in changing landscapes for world crops”, Proceedings of the Royal Society of London B: Biological Sciences 274 (2007) 303.

C. J. Perry, E. Søvik, M. R. Myerscough & A. B. Barron, “Rapid Behavioral Maturation Accelerates Failure of Stressed Honeybee Colonies”, Proceedings of the National Academy of Sciences 112 (2015) 3427.

J. Cascante, M. C. Rojas, A. Salinas, M. Serna, H. D. Torres, E. Vargas, J. Cordovez, J. Arteaga & S. Levis, “Influence of Brood Deaths on Honeybee Population Dynamics and the Potential Impact of Insecticides”, IBIO4299 International Research Experience for Students Ires (2017) (Https://Mcmsc.Asu.Edu/Ires).

K. L. Najib & A. S. Hassan, “Food and environmental degradation as causative agents of honeybee colonies decline: Mathematical model Approach: Journal of Nigerian Society of Physical Sciences 3 (2021) 446. https://doi.org/10.46481/jnps.2021.283

D. C. Schroedor & S. J. Martins, “Deformed Wing Virus”, Virulence 3 (2012) 589.

P. G. Kevan, M. A. Hannan, N. Ostiguy & E. A. Guzman-Novoa, “Summary of the Varroa-virus Disease Complex in Honeybees”, Am Bee J. 146 (2006) 694.

N. Ostiguy, “Honeybee Viruses: Transmission Routes and Interactions with Varroa mites”, 11 Congreso Internacional De Actualizacion Apicola, 9 al 11 De Junio De. Memorias. 47 (2004).

G. Y. Amdam & S. W. Omhoh, “The Regulary Anmomy of Lumeybee Lifespa”, J. Theor. Bio. 216 (2002) 209.

I. Vetharaniam & N. D. Barlow, “Modelling Biocontrol of Varroa-destructor Using a Benign Haplotype as a competitive antagonist”, Available online at: http://www.nzes.org.nz/nzje pg 87-102. Ag Research Limited, Private Bag 3123, Hamilton, New Zealand, Published online: 5 June (2006).

H. F. Abou-Shaara,” Continuous Management of Varroa-mite in Honeybee (Apis Mellifera) Colonies”, Acarina 22 (2014) 149.

A. Denes & M. A. Ibrahim, “Global Dynamics of a Mathematical Model for a HoneybeeColony Infested by Virus-Carrying Varroa Mites”, Journal of Applied Mathematics and Computing (2019). https://doi.org/10.1007/s12190-019-01250-5

K. Messan, G. DeGrandi-Ho man, C. Castillo-Chavez & Y. Kang, “Migration Effects on Population Dynamics of the Honeybee-mite Interactions”, Math. Model. Nat. Phenom 12 (2017) 84. https://doi: 10.1051/mmnp/201712206

V. Ratti, P. G Kevan & H. J. Eberla, “A Mathematical Model of the Honeybee-Varroa Destructor-Acute Bee Paralysis Virus System with Seasonal Effects”, Society for Mathematical Biology 77 (2015) 1493. https://doi:10.1007/s11538-015-0093-5

A. Ishaku, A. M. Gazali, S. A. Abdullahi & N. Hussaini, “Analysis and Optimal Control of an HIV Model Based on CD4 Count”, Journal of Mathematical Biology (2020). https://doi.org/10.1007/s00285-020-01508-8

V. Ratti, P. G., Kevan & H. J. A, Eberl, “Mathematical Model of Forager Loss in Honeybee Colonies Infested with Varroa Destructor and the Acute Bee Paralysis Virus”, Bull. Math. Biol. 79 (2017) 1218. https://doi.org/10.1007/s11538-017-0281-6

A. D´enes & G. R¨ost, “Structure of the Global Attractors in a Model for Ectoparasite- borne Diseases”, Biomath. 1 (2012) 1. https://doi.org/10.11145/j.biomath.2012.09.256

A. D´enes & G. R¨ost, “Global Dynamics for the Spread of Ectoparasite-borne Diseases”, Nonlinear Anal. Real World Appl. 18 (2014) 100. https://doi.org/10.1016/j.nonrwa.2014.01.003

A. D´enes & G. R¨ost, “Dynamics of an Infectious Disease Including Ectoparasites, Rodents and Humans”, Biomathematics: Modeling, Optimization and Computational Problems (2018) 59. https://doi.org/10.1007/978-3-319-91092-55

J. De Figueir´o Santos, F. C. Coelho & P. A. Bliman, “Behavioral Modulation of Infestation by Varroa-destructor in Bee Colonies: Implications for Colony Stability”, PLoS ONE 11 (2016) e0160465. https://doi:10.1371/journal.pone.0160465

O. Sharomi, C. N. Podder, A. B. Gumel & B. Song, “Mathematical analysis of the transmission dynamics of HIV/TB co-infection in the presence of treatment”, Mathematical Biosciences and Engineering 5 (2008) 145.

C. Castillo-Chavez & B. Song, “Dynamical Models of Tuberculosis and their Applications”, Math. Biol. Eng. 1 (2004) 361.

W. Huang, K. L. Cook, & C. Castillo-Chavez, “Stability and Bifurcation for a Multiple-Group Model for the Dynamics of HIV/AIDS Transmission”, SIAM J. Appl. Math. 52 (1992) 835.

J. Dusho , W. Huang & C. Castillo-Chavez, “Backward Bifurcations and Catastrophe in Simple Models of Fatal Diseases”, J. Math. Biol. 36 (1998) 227.

M. Martcheva, “An Introduction to Mathematical Epidemiology, Texts in Applied Mathematics”, ISBN 978-1-4899-7611-6 ISBN 978-1-4899-7612-3 (eBook), Springer Science+Business Media, New York (2015). https://doi:10.1007/978-1-4899-7612-3

P. Van Den Driessche & J. Watmough, “Reproduction Numbers and Sub-Threshold Endemic Equilibria for Compartmental Models of Disease Transmission”, Mathematical Biosciences 180 (2002) 29.

Published

2023-07-09

How to Cite

Analysis of Varroosis Model in Honeybee Colony with Interventions. (2023). African Scientific Reports, 2(2), 98. https://doi.org/10.46481/asr.2023.2.2.98

Issue

Volume 2, Issue 2, August 2023

Section

Original Research
Copyright & Licensing

Copyright (c) 2023 Ahmed Umar, Samuel Musa, Andrew Apeh Agada

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Analysis of Varroosis Model in Honeybee Colony with Interventions. (2023). African Scientific Reports, 2(2), 98. https://doi.org/10.46481/asr.2023.2.2.98