Factorization in Phase-Space Finite Geometry and Weak Mutually Unbiased Bases

Authors

  • A. D. Adeshola Department of Mathematics, Faculty of Science, Gombe State University, Nigeria
  • S. O. Oladejo Department of Statistics and Mathematical Sciences, College of Pure and Applied Science, Kwara State University, Malete, P.M.B. 1530, Ilorin, Nigeria
  • A. O. Abdulkareem Department of Mathematics, Faculty of Science, Lagos State University, Ojo, Nigeria
  • G. R. Ibrahim Department of Statistics and Mathematical Sciences, College of Pure and Applied Science, Kwara State University, Malete, P.M.B. 1530, Ilorin, Nigeria

Keywords:

Non-near-linear Finite geometry, Partial ordering, Factorization

Abstract

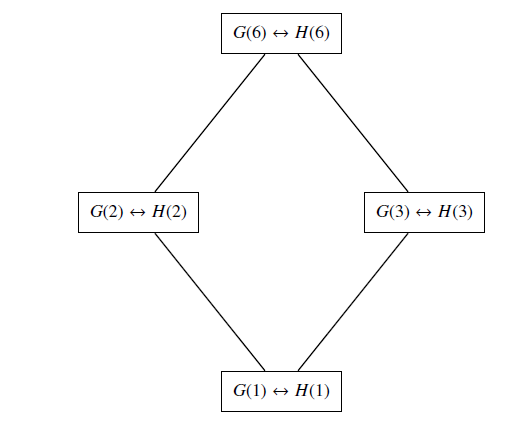
A phase-space factorization of lines in finite geometry G(m) with variables in Zm and its correspondence in finite Hilbert space H(m) for m a non-prime was discussed. Using the method of Good [15], lines in G(m) were factorized as products of lines G(mi) where mi is a prime divisor of m. A lattice was formed between the non trivial sublines of G(m) and lines of G(mi) and between a subspace of H(m) and bases of H(mi) and existence of a link between lines in phase space finite geometry and bases in Hilbert space of finite quantum systems was discussed.

Dimensions

A. Vourdas, “Quantum systems with finite Hilbert space”, Reports on Progress in Physics 67 (2004) 267. https://doi.org/10.1088/0034-4885/67/3/R03

N. Cotfas & J. P. Gazeau, “Finite tight frames and some applications”, Journal of Physics A: Mathematical and Theoretical 43 (2010) 193001. https://doi.org/10.1088/1751-8113/43/19/193001.

T. Durt, B. Englert, I. Bengtsson & Ka. ˙ Zyczkowski, “On mutually unbiased bases”, International journal of quantum information 8 (2010) 535.

J. Tolar & G. Chadzitaskos, “Feynman’s path integral and mutually unbiased bases”, Journal of Physics A: Mathematical and Theoretical 42 (2009) 245306. https://doi.org/10.1088/1751-8113/42/24/245306 Corpus ID: 9968124

L. M. Batten, Combinatorics of finite geometries, Cambridge Univ. Press, Cambridge (1997).

K. S. Gibbons, M. J. Hoffman & W. K. Wootters, “Discrete phase space based on finite fields”, Physical Review A 70 (2004) 062101. https://journals.aps.org/pra/abstract/10.1103/PhysRevA.70.062101

M. Saniga & M. Planat, “Hjelmslev geometry of mutually unbiased bases”, Journal of Physics A: Mathematical and Theoretical 39 (2006) 435. https://doi.org/10.1088/0305-4470/39/2/013

P. ˇ Sulc & J. Tolar, “Group theoretical construction of mutually unbiased bases in Hilbert spaces of prime dimensions”, Journal of Physics A: Mathematical and Theoretical 40 (2007). https://doi.org/10.1088/1751-8113/40/50/013

O. Albouy, “The isotropic lines of Z2 d ”, Journal of Physics A: Mathematical and Theoretical 42 (2009) 072001.

A. Vourdas, “Factorization in finite quantum systems”, Journals of Physics A: Mathematical and Theoretical 36 (2003).

M. Shalaby & A. Vourdas, “Weak mutually unbiased bases”, Journal of Physics A Mathematical and Theoretical 45 (2012) 052001. https://doi.org/10.1088/1751-8113/45/5/052001

M. Shalaby & A. Vourdas, “Mutually unbiased projectors and duality between lines and bases in finite quantum systems”, Annals of Physics 337 (2013) 208. https://doi.org/10.1016/j.aop.2013.06.018

S. O. Oladejo, A. D. Adeshola & A. D. Adeniyi, “Lattice Theory for Finite Dimensional Hilbert Space with Variables in Zd”, Journals of quantum Information Science, 9 (2019) 111. https://doi.org/10.4236/jqis.2019.92006

S. O. Oladejo, C. Lei & A. Vourdas, “Partial Ordering of Weak mutually unbiased Bases”, Journal of Physics A: Mathematical and Theoretical 47 (2014).

I. J Good, “The Relationship Between Two Fast Fourier Transforms”, IEEE C-20 (1971) 310. https://ieeexplore.ieee.org/document/1671829

J. W. P. Hirchfeld, Projective geometries over finite fields, Oxford Univ. Press, Oxford (1979).

H. Havlicek (TUW) & M. Saniga, “Projective Ring Line of an Arbitrary Single Qudit”, Journal of Physics A: Mathematical and Theoretical 41 (2007) 015302.

Published

2023-04-29

How to Cite

Factorization in Phase-Space Finite Geometry and Weak Mutually Unbiased Bases. (2023). African Scientific Reports, 2(1), 96. https://doi.org/10.46481/asr.2023.2.1.96

Issue

Volume 2, Issue 1, April 2023

Section

Original Research
Copyright & Licensing

Copyright (c) 2023 A. D. Adeshola, S. O. Oladejo, A. O. Abdulkareem, G. R. Ibrahim

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Factorization in Phase-Space Finite Geometry and Weak Mutually Unbiased Bases. (2023). African Scientific Reports, 2(1), 96. https://doi.org/10.46481/asr.2023.2.1.96