Application of modified analytical embedded atom method to the study of lattice vibration in bcc transitional metals

Authors

  • Akpata Erhieyovwe
    Department of Physics, Delta State University, Abraka, Delta State Nigeria
  • Ernest Ojegu
    Department of Physics, Delta State University, Abraka, Delta State Nigeria
  • Aroghene Edison Enaibe
    Department of Physics, Federal University of Petroleum Resources, Effurun, Delta State, Nigeria

Keywords:

Transition metal, Lattice dynamics, Nearest neighbour, Modified analytical embedded atom method, Force constant matrix

Abstract

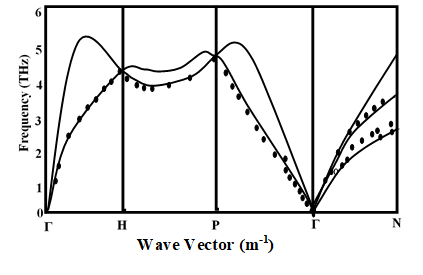
The phonon dispersion curve of four bcc transition metals—(fe), (W), (Mo), and (Cr)—along the principal symmetry [1,0,0], [1,1,1], and [1,1,0] of the Brillouin Zone (BZ) up to the second nearest neighbors is reproduced using the modified analytical embedded atom method (MAEAM) in conjunction with the theory of lattice dynamics. The results obtained are consistent with experimental results, and for all the bcc transition metals taken into consideration, the force constants generated with the MAEAM indicate that the force constants corresponding to the second nearest neighbors were less than the force constants corresponding to the first nearest neighbors. Additionally, the elements of the force constant matrix along φxy, φxz, and φyz are all zero (0). All of the resulting dynamical matrices are diagonal. The generated dispersion curves correlate well with the experimentally generated ones. This demonstrates that the MAEAM is a very dependable instrument for researching the lattice dynamics in bcc transition metals when combined with the theory of lattice dynamics. 

Dimensions

[1] G. Vandana, P. D. Semalty & P. Ram, “Vibrational properties of vacancy in bcc transition metals using embedded atom method potential”, Pramana J. Phys. 80 (2013) 1041. https://doi.org/10.1007/s12043-013-0539-y. DOI: https://doi.org/10.1007/s12043-013-0539-y

[2] O. G. Okocha, Phonon dispersion of some bcc metals, Ph.D. dissertation, Department of Physics, University of Benin, Benin City, Edo State, 2019.

[3] M. I. Baske, “Application of embedded-atom method to covalent materials: A semiempirical potential for silicon”, Phys. Rev. Lett. 59 (1987) 2666. https://doi.org/10.1103/PhysRevLett.59.2666. DOI: https://doi.org/10.1103/PhysRevLett.59.2666

[4] M. W. Finnis & J. E. Sinclair, “A simple empirical N-body potential for transition metals”, Phil. Mag. 50 (1984) 45. https://doi.org/10.1080/01418618408244210. DOI: https://doi.org/10.1080/01418618408244210

[5] M. S. Daw & M. I. Baske, “Semiempirical, quantum mechanical calculation of hydrogen embrittlement in metals”, Phys. Rev. Lett. 50 (1983) 1285. https://doi.org/10.1103/PhysRevLett.50.1285. DOI: https://doi.org/10.1103/PhysRevLett.50.1285

[6] E. Akpata, A. E. Enaibe & A. Iyoha, “Surface energy calculation of low index group 1 alkali metals of the periodic table using the modified analytical embedded atom method”, Int. J. Sci. Res. Eng. Technol. 3 (2014) 876. https://doi.org/10.18488/journal.75/2014.1.1/75.1.34.41.

[7] E. Clementi & C. Roetti, “Roothaan-Hartree-Fock atomic wavefunctions: Basis functions and their coefficients for ground and certain excited states of neutral and ionized atoms, Z ≤ 54”, At. Data Nucl. Data Tables 14 (1974) 177. https://doi.org/10.1016/S0092-640X(74)80016-1. DOI: https://doi.org/10.1016/S0092-640X(74)80016-1

[8] M. S. Daw & M. I. Baske, “Embedded-atom method: Derivation and application to impurities, surfaces, and other defects in metals”, Phys. Rev. B 29 (1984) 6443. https://doi.org/10.1103/PhysRevB.29.6443. DOI: https://doi.org/10.1103/PhysRevB.29.6443

[9] E. Akpata, A. E. Enaibe & S. E. Iyayi, “Comparison of surface energy of bcc alkali metals and transitions using MAEAM”, Rev. Adv. Phys. Theor. Appl. 1 (2014) 34. http://dx.doi.org/10.18488/journal.75/2014.1.1/75.1.34.41 DOI: https://doi.org/10.18488/journal.75/2014.1.1/75.1.34.41

[10] W. Y. Hu, B. W. Zhang, S. L. Shu & B. Y. Huang, “Surface energy calculation of the bcc metals using MAEAM”, J. Alloys Compd. 287 (1999) 159. https://doi.org/10.1016/S0925-8388(99)00043-3. DOI: https://doi.org/10.1016/S0925-8388(99)00024-9

[11] Y. Ouyang, B. Zhang, S. Liao, Z. Jin & H. Chen, “Formation enthalpies for FCC metal based binary alloys by embedded atom method”, Trans. Nonferrous Met. Soc. China 8 (1998) 60. http://www.ysxbcn.com/paper/paperview.aspx?id=paper_15132.

[12] W. Y. Hu, X. L. Shu & B. W. Zhang, “Point-defect properties in bcc transition metals with AEAM interatomic potentials”, Comput. Mater. Sci. 23 (2002) 175. https://doi.org/10.1016/S0927-0256(01)00238-5. DOI: https://doi.org/10.1016/S0927-0256(01)00238-5

[13] Y. Nakagawa & A. D. B. Wood, “Lattice dynamics of niobium”, Phys. Rev. Lett. 11 (1963) 271. https://doi.org/10.1103/PhysRevLett.11.271. DOI: https://doi.org/10.1103/PhysRevLett.11.271

[14] X. You, J. M. Zhang & V. Ji, “MAEAM for phonon dispersion of noble metals in symmetry and off symmetry directions”, Solid State Commun. 145 (2008) 182. https://doi.org/10.1016/j.ssc.2007.10.028. DOI: https://doi.org/10.1016/j.ssc.2007.10.028

[15] G. Venkataraman, L. A. Feldkamp & V. C. Sahni, Dynamics of perfect crystals, MIT Press, Cambridge, USA, 1975. https://mitpress.mit.edu/9780262220194/dynamics-of-perfect-crystals/.

[16] A. Verman, M. Verma & R. P. S. Rathore, “Elastic behavior and lattice vibration in bcc V and Nb”, Acta Phys. Pol. A 90 (1996) 547. http://dx.doi.org/10.12693/APhysPolA.90.547. DOI: https://doi.org/10.12693/APhysPolA.90.547

Published

2025-09-07

How to Cite

Application of modified analytical embedded atom method to the study of lattice vibration in bcc transitional metals. (2025). African Scientific Reports, 4(3), 329. https://doi.org/10.46481/asr.2025.4.3.329

Issue

Volume 4, Issue 3, December 2025 (In Progress)

Section

PHYSICS SECTION
Copyright & Licensing

Copyright (c) 2025 Akpata Erhieyovwe, Ernest Ojegu, Aroghene Edison Enaibe

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Application of modified analytical embedded atom method to the study of lattice vibration in bcc transitional metals. (2025). African Scientific Reports, 4(3), 329. https://doi.org/10.46481/asr.2025.4.3.329