An Inertial Algorithm of Generalized f -Projection for Maximal Monotone Operators and Generalized Mixed Equilibrium Problems in Banach Spaces

Authors

  • Lawal Umar Department of Mathematics, Federal College of Education, Zaria, Kaduna, Nigeria
  • Tafida M. Kabir Department of Mathematics, Federal College of Education, Zaria, Kaduna, Nigeria
  • Ibrahim U. Haruna Department of Mathematics, Federal College of Education, Zaria, Kaduna, Nigeria

Abstract

In this paper, we study a modified hybrid inertial algorithm of generalized f-projection for approximating maximal monotone operators and solutions of generalized mixed equilibrium problems in Banach spaces. Our results generalize and improve many recent announced results in the literature.

Dimensions

B. T. Polyak, “Some methods of speeding up the convergence of iteration methods”, USSR Comput. Math. Phys. 4 (1964) 1.

R. I. Bot, & E.R. Csetnek, “An inertial forward-backward -forward primal-dual splitting algorithm for solving monotone inclusions problems”, Numer Algorithms 71 (2016) 519.

R. I. Bot, E.R. Csetnek, & C. Hendrich, “Inertial Douglas-Racheord splitting for monotone inclusion problems”, Appt. Math. Comput. 256 (2015) 472.

C.E.Chidume, S.I. Ikechukwu, & A.Adamu, “Inertial algorithm for approximating a common fixed point for a countable family of relatively nonexpansive maps”, Fixed Point Theory and Application 9 (2018) 16.

C. E. Chidume, P. Kumam, & A. Adamu, “A hybrid Inertial algorithm for approximating solution of convex feasibility problems with applications”, Fixed point theory and application 12 (2020) 17.

B. Ali, & L. Umar, “Approximation of solution of generalized mixed equilibrium problems and fixed points of multivalued asymptotically quasi-nonexpansive mappings”, Journal of the Nigerian Mathematical Society. 38 (2019) 569.

E. Blum & W.Oettli, “From optimization and variational inequalities to equilibrium problems”, Math. Stud. 63 (1994) 123.

L. C. Ceng, & J. C. Yao, “A hybrid iterative scheme for mixed equilibrium problem and fixed point problem”, J. Comput. Appl. Math. 214 (2008) 186.

B. A. Bin Dehaish, A. Latif, H. O. Bakodah & X. Qin, “A regularization projection algorithm for various problems with nonlinear mappings in Hilbertspaces”, J. Inequal. Appl. 1 (2015) 51.

S. Y. Cho, “Generalized mixed equilibrium and fixed point problems in Banach spaces”, J. Nonlinear Sci. Appl. 9 (2016) 1083.

X. Qin, & J. C. Yao, “Projection splitting algorithm for nonself operators”, J. Nonlinear Convex Anal. 18 (2017) 925-935.

B. Martinet, “Regularisation d inequations variationelles par approximations succesives”, Rev. Fr. Inf. Rech. Oper. 2 (1970) 154.

M. V. Solodov & B. F. Svaiter, “Forcing strong convergence of proximal point iterations in Hilbert spaces”, Math. Program. 87 (2000) 189.

S. Kamimura, & W. Takahashi, “Approximating solutions of maximal monotone operators in Hilbert spaces”, J. Approx. Theory. 106 (2000) 226.

F. Kohsaka, & W. Takahashi, “Strong convergence of an iterative sequence for maximal monotone operators in a Banach spaces”, Abstract and Applied Analysis 3 (2004) 239.

Y. I. Alber, Metric and generalized projection operators in Banach spaces: properties and applications, in: A.G. Kartsatos (Ed.) Theory and Applications of Nonlinear Operators of Accretive and Monotone Type, Marcel Dekker, New York, (1996).

Y. I. Alber, “Generalized projection operators in Banach spaces: properties and applications, in: Proceedings of the Israel Seminer, Ariel, Israel”, Funct. Differential Equation. 1 (1994) 1.

J. L. Li, “The generalized projection operator on reflexive Banach spaces and its applications”, J. Math. Anal. Appl. 306 (2005) 55.

X. Li, N. Huang, & D. O’Regan “Strong convergence theorem for relatively nonexpansive mappings in Banach spaces with applications”, Comp. Math. App. 60 (2010) 1322.

S. Saewan, & P. Kumam, “A generalized f-projection method for countable families of weak relatively nonexpansive mappings and system of generalized Ky Fan inequalities”, J. Glob Optim, (2012) DOI 10.1007/s10898-012-9922-3.

C. E. Chidume, M. O. Nnakwe, & A. Adamu, “A strong convergence theorem for generalized φ-strongly monotone maps with applications”, Fixed Point Theory and Application 11 (2019) 19.

A. A. Hammad, A.A.Mebawandu, O.K. Narain & J. K. Kim, “Outer approximation method for zero of sum of monotone operators and fixed point problems in Banach spaces”, Nonlinear Functional Analysis and Applications 20 (2021) 451.

S. Saewan, “New convergence theorems for maximal monotone operators in Banach space”, International Journal of Mathematics and Computer in Simulation 15 ( 2021), DOI: 46300/9102.2021.15.2.

I. Yusuf, “Strong convergences for split common fixed point problem of Bregman generalized asymptotically nonexpansive mappings in Banach spaces”, Journal of the Nigerian Society of physical Sciences 1 (2019) 35.

C.Klin, S. Suantai, & W. Takahashi, “Strong convergence of generalized projection algorithms for nonlinear operators”, Abstract and Applied Analysis (2009), doi:10.1155/2009/649831.

S. Saewan, & P. Kumam, “Convergence theorems for uniformly quasi -φ-asymptotically nonexpansive mappings, generalized equilibrium problems and variational inequalities in Banach space”, Fixed Point Theory and Application 96( 2011) 18.

W. Takahashi, Nonlinear Functional Analysis, Yokohama publishers, Yokohama (2000).

V.Darvish ,“ Strong convergence theorem for a system of generalized mixed equilibrium problems and finite family of Bregman nonexpansive mappings in Banach spaces”, Opearch 53 (2016) 584.

S. S. Zhang, “Generalized mixed equilibrium problem in Banach spaces”, Appl. Math. Mech. 30 (2009) 1105.

S. Kamimura, & W. Takahashi, “Strong convergence of a proximal-type algorithm in a Banach space”, SIAM J, Optim. 13 (2002) 938-945.

K. Q. Wu, & N. J. Huang, “The generalized f-projection operator with application”, Bull. Aust. Math. Soc. 73 (2006) 307.

J. H. Fan, X. Liu, & J. L. Li, “Iterative schemes for approximating solutions of generalized variational inequalities in Banach spaces”, Nonlinear Anal. TMA 70 (2009) 3997.

K. Deimling, Nonlinear Functional Analysis, Spriger-Veriag. Berlin. Heideiberg. New York, Tokyo, (1985).

H.Zegeye, “A hybrid iterative scheme for equilibrium problems, variational inequality problems and common fixed point problems in Banach spaces”, Nonlinear Anal. 72 (2010) 2136.

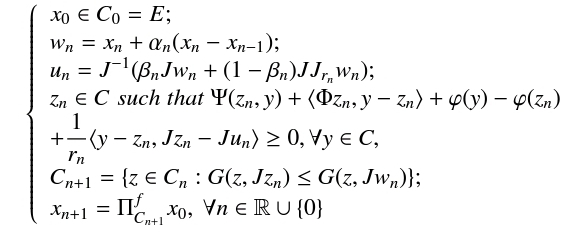
Published

2022-04-29

How to Cite

An Inertial Algorithm of Generalized f -Projection for Maximal Monotone Operators and Generalized Mixed Equilibrium Problems in Banach Spaces. (2022). African Scientific Reports, 1(1), 32-47. https://doi.org/10.46481/asr.2022.1.1.22

Issue

Volume 1, Issue 1, April 2022

Section

Original Research
Copyright & Licensing

Copyright (c) 2022 Lawal Umar, Tafida M. Kabir, Ibrahim U. Haruna

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

An Inertial Algorithm of Generalized f -Projection for Maximal Monotone Operators and Generalized Mixed Equilibrium Problems in Banach Spaces. (2022). African Scientific Reports, 1(1), 32-47. https://doi.org/10.46481/asr.2022.1.1.22