Mathematical modelling of terrorists re-cycle induced with backward bifurcation
Abstract
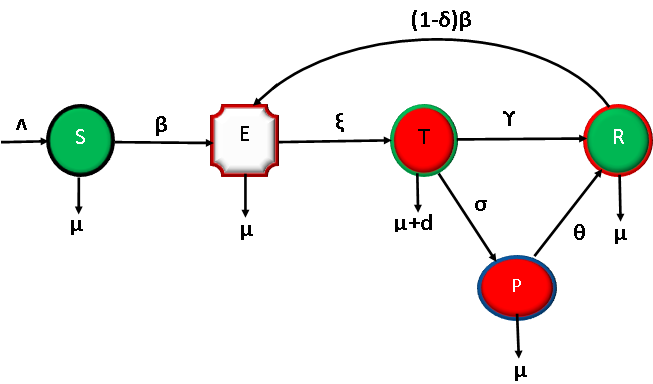
In this work, we formulate a deterministic mathematical model that aims at controlling and preventing terrorism in a population. The model incorporates the prevention of the spread of terrorists in the population by imprisoning individuals caught in the act and allows for natural repentance from terrorism. The main aim of the study is to assess the effect of re-cycling terrorists on the bifurcation phenomena of the model. The model exhibits a backward bifurcation phenomenon. These may have serious implications for the design of intervention programs aiming at eradicating the menace of terrorism. When the values of the scaling factor of the re-cycling rate change from 0 to 1, the bifurcation changes from backward to forward. One or more stable endemic equilibria coexist alongside the stable terrorists-free equilibrium (TFE). It is further demonstrated that the recycling of terrorists who have repented from the terrorism act is what triggers the backward bifurcation cycle. This conclusion is important because it shows that eliminating terrorists from the population is no longer dependent on the old precondition of the basic reproduction number being less than one. The parameter of recycling is deleted, and the model is examined, to determine the reason why this model exhibits a backward bifurcation phenomenon. By taking into account the importance of the original model, this was made achievable. When the terrorists aren’t recycled, the second model will demonstrate a forward bifurcation, according to an analysis of the second model’s coefficient of bifurcation, which is negative.
Published
How to Cite
Issue
Section
Copyright (c) 2023 Rwat Solomon Isa, Tsok Samuel Hwere, Usman Garba, Shehu Sidi Abubakar, Sabastine Emmanuel

This work is licensed under a Creative Commons Attribution 4.0 International License.




