Numerical simulation of a nonlinear diffusion type equation in a two phase media with linear porosity and permeability model

Authors

  • I. D. Dorothy
    Department of Physics, Joseph Sarwuan Tarka University, Makurdi, Benue-Nigeria
  • I. M. Echi
    Department of Physics, Joseph Sarwuan Tarka University, Makurdi, Benue-Nigeria
  • A. N. Amah
    Department of Physics, Joseph Sarwuan Tarka University, Makurdi, Benue-Nigeria

Keywords:

Permeability, Porosity, Nonlinear pressure diffusion equation, Numerical simulation

Abstract

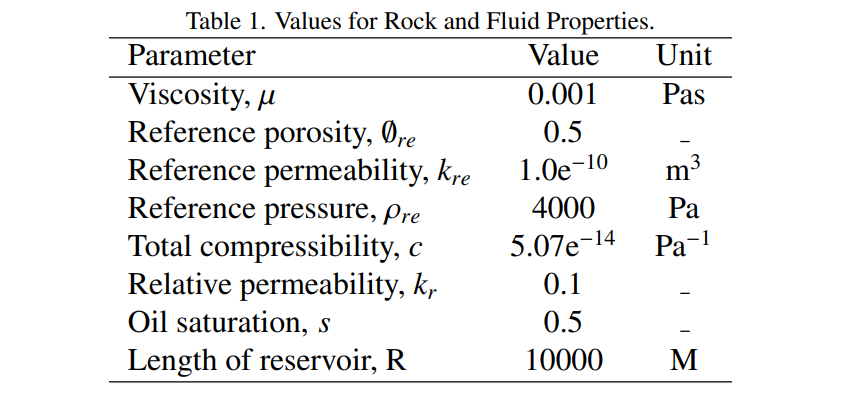
Predicting and understanding the behavior of pressure is important in reservoir maintenance and evaluation. This work studies the behavior of fluid pressure in a reservoir by numerical simulation of the pressure diffusion type equation in a two phase media with a linear porosity and permeability model. Because the porosity and permeability are pressure dependent, the resulting diffusion type equation is nonlinear and is solved using a backward-forward finite difference method. The simulation code was ran using a constant porosity and permeability model and a linear porosity and permeability model. The results from the linear porosity and permeability model was compared to that of the constant porosity and permeability model. In both cases the pressure gradient was greatest at the wellbore and decreases as the radial distances away from the wellbore increases. The pressure in both cases also decreased with time. However, at each location and time the pressure drop was lower in the linear porosity and permeability model than with the constant porosity and permeability. The backward-forward finite difference method proved to be useful in solving numerically the nonlinear diffusion type equation. This work can be applied in the oil and gas industry to predict pressure behavior in reservoirs and make investment decisions, production and maintenance decision.

Dimensions

Y. Jin & K. Chen, “Fundamental equations for primary fluid recovery from porous media”, Journal of fluid Mechanics 860 (2019) 300. https://doi.org/10.1017/jfm.2018.874

L. Yan, D. P. Jonathan, A. W. David & E. Bruce, “Nonlinear pressure diffusion in a porous medium. Approximate solutions with applications to permeability measurements using transient pulse decay method”, Journal of Geophysical Research: Solid Earth 106 (2001) B1. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2000JB900344

V. K. Evgenii, S. T. Mikhail, P. R. Evgenii & V. P. Vladimir, “Effect of effective pressure on the permeability of rocks based on well testing results”, Energies 14 (2021) 8. https://doi.org/10.3390/en14082306

E. Selcuk, S. J. Fowler, H. Virginie, & L. Ben, “An analytical model of porosity-permeability for porous and fractured media”, Transport in Porous Media 120 (2017) 327. https://doi.org/10.1007/s11242-017-0923-z

L. Chunguang, S. Guanhua, G. Mingwei & W. Shuilin, “Permeability of porous media under confining pressure”, Geophysics Journal International 216 (2019) 3. https://doi.org/10.1093/gji/ggy531

A. E. Scheidegger, The physics of flow through porous media (3rd Edition), University of Toronto Press, Toronto, (2020), pp. 1-53. https://www.degruyter.com/document/doi/10.3138/9781487583750/html

L. Shen, T. Cui, H. Liu, Z. Zhu, H. Zhong, Z. Chen, B. Yang, R. He & H. Liu, “Numerical simulation of two-phase flow in naturally fractured reservoirs using dual porosity method on parallel computers”, Proceedings of the International Conference on High Performance Computing in Asia Pacific Region, Guangzhou, China, (2019), pp. 91-100. https://doi.org/10.1145/3293320.3293322

S. Gasmi, & F.Z. Nouri, “Numerical simulation for two phase flow in a porous medium”, Boundary Value Problem 2015 (2015) 7. https://doi.org/10.1186/s13661-014-0256-6 Numerical Treatment of Two-phase Flow in Porous Media Including Specific Interfacial Area

M. El-Amin, J. Kou, A. Salama & S. Sun, “Numerical treatment of two-phase flow in porous media including specific interfacial area”, Science Direct 51 (2015) 53. https://doi.org/10.1016/j.procs.2015.05.306

M. C. Jose, P. Stefano, J. Santos, N. Ayman, N. A. Qadrouh & H. Almalki, “Numerical simulation of two phase fluid flow”, Journal of Petroleum Exploration and Production Technology 4 (2014) 233. https://doi.org/10.1007/s13202-014-0109-y

C. G. Nmebu, “Modelling the pressure distribution in a reservoir undergoing MEOR for a 2-dimensional flow system”, International journal of Emerging Technology and Advanced Engineering 4 (2014) 6. https://www.researchgate.net/publication/263315861 Modeling the Pressure Distribution in a Reservoir Undergoing MEOR for a 2-Dimensional Flow System

A. Opoku, K. D. Ohenewaa & T. B. Eric, “A Comparative study between finite difference explicit and implicit method for predicting pressure distribution in a petroleum reservoir”, International Journal of Engineering science and Technology 11 (2019) 23. https://doi.org/10.4314/ijest.v11i4.3

Z. Chen, G. Huan & Y. Ma, “Computational methods for multiphase flows in porous media”, Computational Science and Engineering Series, Philadelphia, PA, USA, (2006), pp. 1-282. https://doi.org/10.1137/1.9780898718942

M. K. Jain, S. R. K. Iyengar & R. K. Jain, “Computational methods for partial differential equations”, 2nd Edition, Newyork, New Age International Publishers (2016) 240. https://www.amazon.com/Computational-Methods-for-Partial-Differential-Equations/dp/812243973X

L. B. Winrich, An Explicit method for numerical solution of a nonlinear diffusion equation, Ph.D. dissertation, Mathemat ics Department, Iowa State University of Science and Technology, Ames, Iowa, 1968. https://dr.lib.iastate.edu/entities/publication/a132deb4-9568-4883-aa63-e828f9eef9b0

S. Schmelter & M. Bar, “Numerical simulation validation and analysis of two phase slug flow in large horizontal pipes”, Journal of Flow Measurement and Instrumentation 73 (2020) 101722. https://www.sciencedirect.com/science/article/pii/S0955598620300704

T. Ahmed & P. D. McKinney, Advanced reservoir engineering (1st Edition), Oxford, Gulf Professional Publishing, Elsevier, Burlington, United states of America, (2005), pp. 1-363. https://doi.org/10.1016/B978-0-7506-7733-2.X5000-X

M. A. Abdullah, A. Panda, S. Gupta, S. Joshi, A. Singh, & N. Rao, “Multi-scale method for modeling and simulation of two phase flow in reservoir using MRST”, Petroleum and Coal 61 (2019) 3. https://research.vit.ac.in/publication/multi-scale-method-for-modeling-and-simulation-of-two-phase-flow-1

Values for Rock and Fluid Properties.

Published

2024-02-01

How to Cite

Numerical simulation of a nonlinear diffusion type equation in a two phase media with linear porosity and permeability model. (2024). African Scientific Reports, 3(1), 119. https://doi.org/10.46481/asr.2024.3.1.119

Issue

Volume 3, Issue 1, April 2024

Section

PHYSICS SECTION
Copyright & Licensing

Copyright (c) 2024 I. D. Dorothy, I. M. Echi, A. N. Amah

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Numerical simulation of a nonlinear diffusion type equation in a two phase media with linear porosity and permeability model. (2024). African Scientific Reports, 3(1), 119. https://doi.org/10.46481/asr.2024.3.1.119

Similar Articles

1-10 of 39

You may also start an advanced similarity search for this article.