Coding Matrices for Wreath Products of Groups

Authors

  • Enoch Suleiman Department of Mathematics, Federal University Gashua, Yobe State, Nigeria
  • Ahmed A. Khammash Department of Mathematical Sciences, Umm Al-Qura University, Makkah, Saudi Arabia

Keywords:

Code, Ring of matrices, Group ring, Wreath product, Semi direct product, Matrix

Abstract

Wreath product, a powerful construction in group theory, has found extensive applications in various areas of mathematics and computer science. In this paper, we present a comprehensive analysis of coding matrices associated with wreath products. The coding matrices for the wreath product of two cyclic finite groups were given for the first time. It gives a generalization of the coding matrices for the semi-direct product. We found out that the coding matrix of wreath product really has the same shape as the one for semidirect product and gave the RW-matrix for the coding matrix. An example was showed to illustrate the assertions. Conditions were also given for different wreath products of cyclic groups and that gives different orders for the wreath products.

Dimensions

T. Hurley, “Group Rings and Rings of Matrices”, International Journal of Pure and Applied Mathematics 31 (2006) 319.

P. Hurley & T. Hurley, “Codes from Zero-divisors and Units in Group Rings” arXiv:0710.5893v1 [cs.IT] (2007) 1.

T. Hurley, “Convolutional codes from units in matrix and group rings”, arXiv:0711.3629v1 [cs.IT] (2007) 1.

P. Hurley & T. Hurley, “Block codes from matrix and group rings”, In P. Hurley, & T. Hurley, Chapter 5, in Selected topics in information

and coding theory, (2010) 159.

M. M. Hamed & A. A. Khammash, “Coding Matrices for GL(2,q)”, Fundamental Journal of Mathematics and Applications 1 (2018) 118.

A. A. Alkinani & A. A. Khammash, “Coding Matrices for the Semi-Direct Product Groups”, Fundamental Journal of Mathematics and Applications 3 (2020) 109. https://doi.org/10.33401/fujma.690424

T. Rhian, Group rings: Units and their applications in self-dual codes, PhD Thesis, University of Chester (2022).

J. D. Dixon, & B. Mortimer, Permutation Groups, Springer, Berlin, New York (1996).

B. Sury, “Wreath Products, Sylow’s Theorem and Fermat’s Little Theorem”, European Journal of Pure and Applied Mathematics 3 (2010) 13.

E. Suleiman & M. S. Audu, “Some Embedment of Groups into Wreath Products”, International Journal of Algebra and Statistics 9 (2020) 1. https://doi.org/10.20454/ijas.2020.1630

Z. S.Tan, Cyclic And Dihedral Group Ring Codes, MSc Thesis, Universiti Sains Malaysia (USM) (2016).

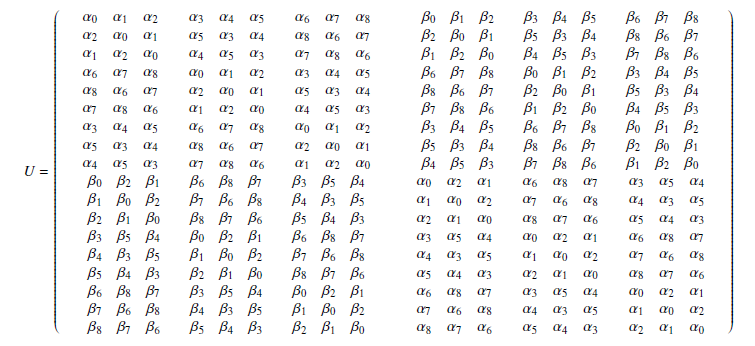
Published

2023-07-11

How to Cite

Coding Matrices for Wreath Products of Groups. (2023). African Scientific Reports, 2(2), 114. https://doi.org/10.46481/asr.2023.2.2.114

Issue

Volume 2, Issue 2, August 2023

Section

Original Research
Copyright & Licensing

Copyright (c) 2023 Enoch Suleiman, Ahmed A. Khammash

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

Coding Matrices for Wreath Products of Groups. (2023). African Scientific Reports, 2(2), 114. https://doi.org/10.46481/asr.2023.2.2.114